ROC与AUC

发表于   |   分类于 ，   |  

这篇文章只要是介绍分类算法评估标准，介绍标准之前首先介绍一下评价算法的前提，混淆矩阵，如图

混淆矩阵
目前常用的评价一个分类算法好坏的标准有：

  1. Accuracy：表示预测结果的精确度，预测正确的样本数除以总样本数。（TP+TN）/(TP+FP+FN+TN)
  2. precision，准确率，表示预测结果中，预测为正样本的样本中，正确预测为正样本的概率；TP/(TP+FP)
  3. recall，召回率，表示在原始样本的正样本中，最后被正确预测为正样本的概率；TP/(TP+FN)
  4. specificity，常常称作特异性，它研究的样本集是原始样本中的负样本，表示的是在这些负样本中最后被正确预测为负样本的概率。TN/(FP+TN)
    还有就是这篇文章里面要介绍的ROC曲线和AUC

什么是ROC？

ROC全称Receiver Operating Characteristic,翻译为”接受者操作特性曲线”,即ROC为二维平面上的一条曲线，
横坐标：FPR 假阳率（1-sp） =FP/(TN+FP)
纵坐标：TPR 真阳率（ recall ）= TP/(TP+FN)
如图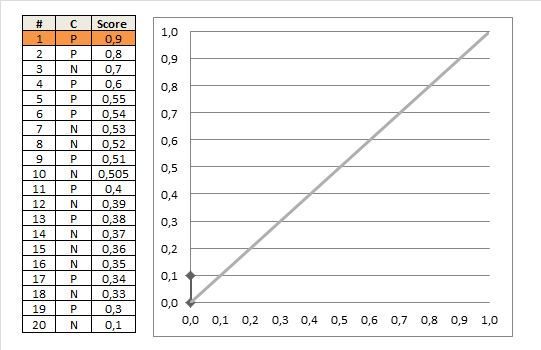
ROC曲线

ROC曲线有什么优点？

提供不同试验之间在共同标尺下的直观的比较，ROC曲线越凸越近左上角表明其诊断价值越大，利于不同指标间的比较。该方法简单、直观，通过图示可观察分析方法的临床准确性，并可用肉眼作出判断。

什么是AUC

AUC的值就是处于ROC curve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的performance。
0.5~0.7之间时有较低准确性
0.7~0.9之间有一定准确性
0.9以上有较高准确性。

AUC

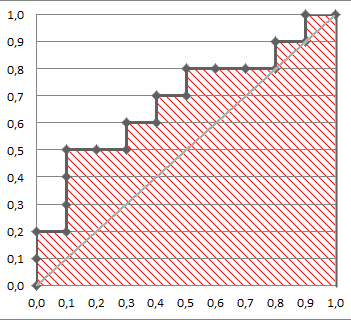
AUC计算方式

  1. 积分的思想，逐步求面积
  2. 一个关于AUC的很有趣的性质是，它和Wilcoxon-Mann-Witney Test是等价的。Wilcoxon-Mann-Witney Test就是测试任意给一个正类样本和一个负类样本，正类样本的score有多大的概率大于负类样本的score。
    统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2 )。n为样本数(即n=M+N)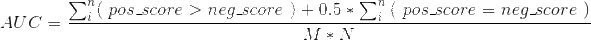
    AUC
  3. 方法二的简化，首先把所有样本按照score排序,依次用rank表示他们,如最大score的样本,rank=n(n=N+M),其次为n-1。那么对于正样本中rank最大的样本,rank_max,有M-1个其他正样本比他score小,那么就有(rank_max-1)-(M-1)个负样本比他score小。其次为(rank_second-1)-(M-2)
    AUC

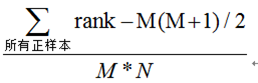
ROC与AUC与其他评价方法相比的好处？

ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。